二 项目流程

转录组和蛋白质组的关联分析云流程包含了以下数据分析方法。

三 数据分析结果

在该部分为您简述云流程涉及到的方法及分析结果

3.1 数据预处理

除可变剪切和不编码蛋白质等情况外，蛋白质组数据应该与转录组数据一一对应。但转录组测序通常能覆盖几乎整个转录组而蛋白质组质谱分析的覆盖度通常低于转录组（尤其对于低丰度蛋白、膜蛋白、极端大小/电荷蛋白），导致许多检测到的 mRNA 没有对应的蛋白数据。该步骤能够依据用户输入对转录组和蛋白质组数据进行匹配和转化，删除无法对应ID的数据并使用Venn图统计。本项目结果图见结果文件 01_数据预处理/本部分包含以下结果：
├── 01_数据预处理
├── procSelect [和转录组数据对应的蛋白质组数据，您可以将其导入Excel查看并编辑]
├── transSelect [和蛋白质组数据对应的转录组数据。注意转录组的id已经转化为uniprot AC，您可以将其导入Excel查看并编辑]
└── Venn.svg [相关性热图]

3.2 转录组和蛋白质组数据的相关性热图

分析单个基因的 mRNA 与其对应蛋白在不同样本或条件下的丰度变化趋势是否一致。可以识别出哪些基因的转录-翻译关系是稳定的，哪些是受调控的。
02_相关性热图/本部分包含以下结果：
├── 02_相关性热图
├── r_result.tsv
├── p_result.tsv
└── corrHeatmap.svg [相关性热图]

3.3 转录组和蛋白质组的九象限图

九象限图能够揭示单个基因的 mRNA 与其对应蛋白在不同样本或条件下的丰度变化趋势是否一致。可以识别出哪些基因的转录-翻译关系是稳定的，哪些是受调控的。其中：
第3、第7象限代表一致差异，既在 mRNA 和蛋白水平均显著上调或下调的基因/蛋白。这些是功能变化最直接的候选者。
第2、第8象限代表mRNA 变，蛋白不变： 可能受翻译抑制或蛋白质稳定性增加调控。
第4、第6象限代表mRNA 不变，蛋白变： 可能受翻译效率提高或蛋白质稳定性降低调控。 第1、第9象限代表方向相反： mRNA 上调但蛋白下调（如快速降解），或 mRNA 下调但蛋白上调（如翻译激活）。 03_九象限图/本部分包含以下结果：
├── 03_九象限图
├── procSelect [和转录组数据对应的蛋白质组数据，您可以将其导入Excel查看并编辑]
├── transSelect [和蛋白质组数据对应的转录组数据。注意转录组的id已经转化为uniprot AC，您可以将其导入Excel查看并编辑]
└── quardant.svg [九象限图]

3.4 多元统计模型分析

基于多元统计（降维、潜变量）的方法提供了更好的对转录组和代谢组数据进行探索性分析，能够突出显示两组学之间的全局相关性，以及找出单个组学数据中的异常值或批次效应，还有助于处理和基因/代谢物的下游分析^[15]。这里对本流程中的涉及的多元统计分析方法（包括CCA, PLS, PLS-DA, O2PLS）进行简要描述。

为了使表达一致，首先对不同文献中的公式符号记法进行统一。在本节出现的公式中进行如下约定：大写加粗的字母（例如\(\boldsymbol{X}\)）表示矩阵，小写加粗的字母（例如\(\boldsymbol{f}\)）表示向量，而小写不加粗的字母（例如\(n,p\)）表示标量。

许多数学对象可以通过将它们分解成多个组成部分或者找到它们的一些通用的属性来更好的理解。给定一个组学数据集 \(\boldsymbol{X}\)，它是一个\(n \times p\)矩阵，由\(n\)个观测值（也就样本数）和\(p\)个变量（也就是基因或代谢物的数量）组成，它可以用以下形式表示： $$\boldsymbol{X} = (\boldsymbol{x}_1,\boldsymbol{x}_2,\cdots,\boldsymbol{x}_p)$$ 注意，该式中每个\(\boldsymbol{x}\)都是一个\(n\)维向量，包含了\(n\)个样本的测量值（基因表达量或代谢物丰度）。大多数情况下，组学研究的变量数远大于样本数量\(p>>n\)，也就是基因/代谢物的数量远大于样本数。我们需要找到一组新的变量，这些新的变量由原始数据的线性组合组成并且能够捕获原始数据中的绝大部分方差。通常，这些变量被称为隐变量（Latent Variable）或被称成分（Component）。其中一个隐变量\(\boldsymbol{f}\)可以由以下公式表示： $$\boldsymbol{f}=q_1 \boldsymbol{x}_1+q_2 \boldsymbol{x}_2+\cdots+q_p \boldsymbol{x}_p$$ 此处，\(\boldsymbol{f}\)是\(n\)维向量。该式也可以转化为矩阵向量乘法的形式： $$\boldsymbol{f} = \boldsymbol{X}\boldsymbol{q}$$ 该式中系数向量\(\boldsymbol{q} = (q_1,q_2,\cdots,q_p)^T\)控制原始组学数据集的每个变量的缩放，被称作载荷（loading）。隐变量的数量远远小于\(p\)。通过将原始组学数据矩阵分解的形式，少量的隐变量即能够描述整个组学数据。

3.4.1 CCA分析

对一组数据降维的方法可以拓展到多组数据。包括协惯量分析（Co-Inertia Analysis， CIA），偏最小二乘分析（Partial Least Squares, PLS），典型对应分析（Canonical Correspondence analysis, CCA）和典型相关分析（Canonical Correlation Analysis , CCA）等方法。需要注意的是典型对应分析和典型相关分析的英文缩写均为CCA。典型对应分析是对应分析（Correspondence analysis， CA）的一种约束形式，它广泛应用于生态学方向的研究却并未广泛运用于多组学关联分析^[15]。本流程用CCA表示典型相关分析。

在CCA分析中，两个组学数据集 \(\boldsymbol{X}\)（维度为 \(n \times p_1\)） 和\(\boldsymbol{Y}\)（维度为 \(n \times p_2\)）可以用以下隐变量分解的形式表示： $$\boldsymbol{X}=\boldsymbol{F}_x \boldsymbol{Q}_x^T+\boldsymbol{E}_x\\\boldsymbol{Y}=\boldsymbol{F}_y \boldsymbol{Q}_y^T+\boldsymbol{E}_y $$ 式中\(\boldsymbol{F}_x\)和\(\boldsymbol{F}_y\)为维度为\(n \times r\)维矩阵，该矩阵包含r个的隐变量（成分），每个隐变量是n维向量。隐变量矩阵\(\boldsymbol{F}_x\)和 \(\boldsymbol{F}_y\)解释了两个组学数据的共同结构（co-structure）。\(\boldsymbol{Q}_x\) 和\(\boldsymbol{Q}_y\)是\(\boldsymbol{F}_x\) 和 \(\boldsymbol{F}_y\)的载荷，而\(\boldsymbol{E}_x\)和\(\boldsymbol{E}_y\)代表误差项。CCA分析通过最大化\(\boldsymbol{Xq}_x^i\)和\(\boldsymbol{Yq}_y^i\)的相关性来获得组学数据集 \(\boldsymbol{X}\)和\(\boldsymbol{Y}\)的相关性。

然而在进行CCA分析时，由于需要计算隐变量相关性矩阵的逆矩阵，因此无法直接在变量数远大于样本数量的组学数据集的分析中使用^[16]。一些CCA分析的变体可以解决上述问题从而使其可以使用在两个组学的关联分析中。例如Sparse CCA（sCCA）^[1],[17]来进行多组学关联分析。 本项目结果图见结果文件 04_CCA分析/

本部分包含以下内容：
├── 04_CCA分析
├── arrow.svg [转录组和代谢组隐变量关联散点图]
├── biplot.svg [双序图]
├── plotVar.svg [相关性圈图]
└── scatter.svg [载荷图]

图3.5 CCA分析

注：（a）CCA分析双序图，该图具有两套原点和单位向量方向相同的坐标系。图中散点代表隐变量而箭头代表载荷。散点表示样本在PC1和PC2轴上的隐变量的贡献度，对应Component坐标系（左下坐标轴）；从原点出发的箭头的端点表示载荷值，对应Eigenvector of Component坐标系（右上）。其生物学意义的解析见结题报告3.3.5 重要的图的解读；（b）隐变量散点图，其中Block1和Block2分别代表转录组和代谢组，散点表示样本在PC1和PC2轴上隐变量的贡献度；（c）同一隐变量对转录组和代谢组分别的贡献；（d）相关性圈图，代表载荷的分布情况。

3.4.2 PLS分析

PLS是高维组学数据分析中的另外一种高效降维方法。同CCA类似，PLS也使用隐变量分解的方式对两组学数据集降维并寻找其共同结构，但PLS最大化协方差矩阵而不是隐变量间的相关性^[18]。这种方式使得PLA的结果更加稳健并能够更好的处理极端值的影响，同时，PLS法不会像CCA一样遭遇\(p≫n\)时无法求解的问题。本项目结果图见结果文件 05_PLS分析/

本部分包含以下内容：
├── 05_PLS分析
├── arrow.svg [转录组和代谢组隐变量关联散点图]
├── biplot.svg [双序图]
├── plotVal.svg [相关性圈图]
└── scatter.svg [载荷图]

图3.6 PLS分析

注：（a）PLS分析双序图，该图具有两套原点和单位向量方向相同的坐标系。图中散点代表隐变量而箭头代表载荷。散点表示样本在PC1和PC2轴上的隐变量的贡献度，对应Component坐标系（左下坐标轴）；从原点出发的箭头的端点表示载荷值，对应Eigenvector of Component坐标系（右上）。其生物学意义的解析见结题报告3.3.5 重要的图的解读；（b）隐变量散点图，其中Block1和Block2分别代表转录组和代谢组，散点表示样本在PC1和PC2轴上隐变量的贡献度；（c）同一隐变量对转录组和代谢组分别的贡献；（d）相关性圈图，代表载荷的分布情况。

3.4.3 O2PLS分析

不同类型的组学研究在规模，分布形状，实验误差等方面存在差异，而上文中提到的CCA和PLS并为考虑不同组学特有的变异。在构建模型时将不同组学特有的变异纳入模型，可能会使得模型的性能更好^[19]。O2PLS算法正是基于这种思想被提出。

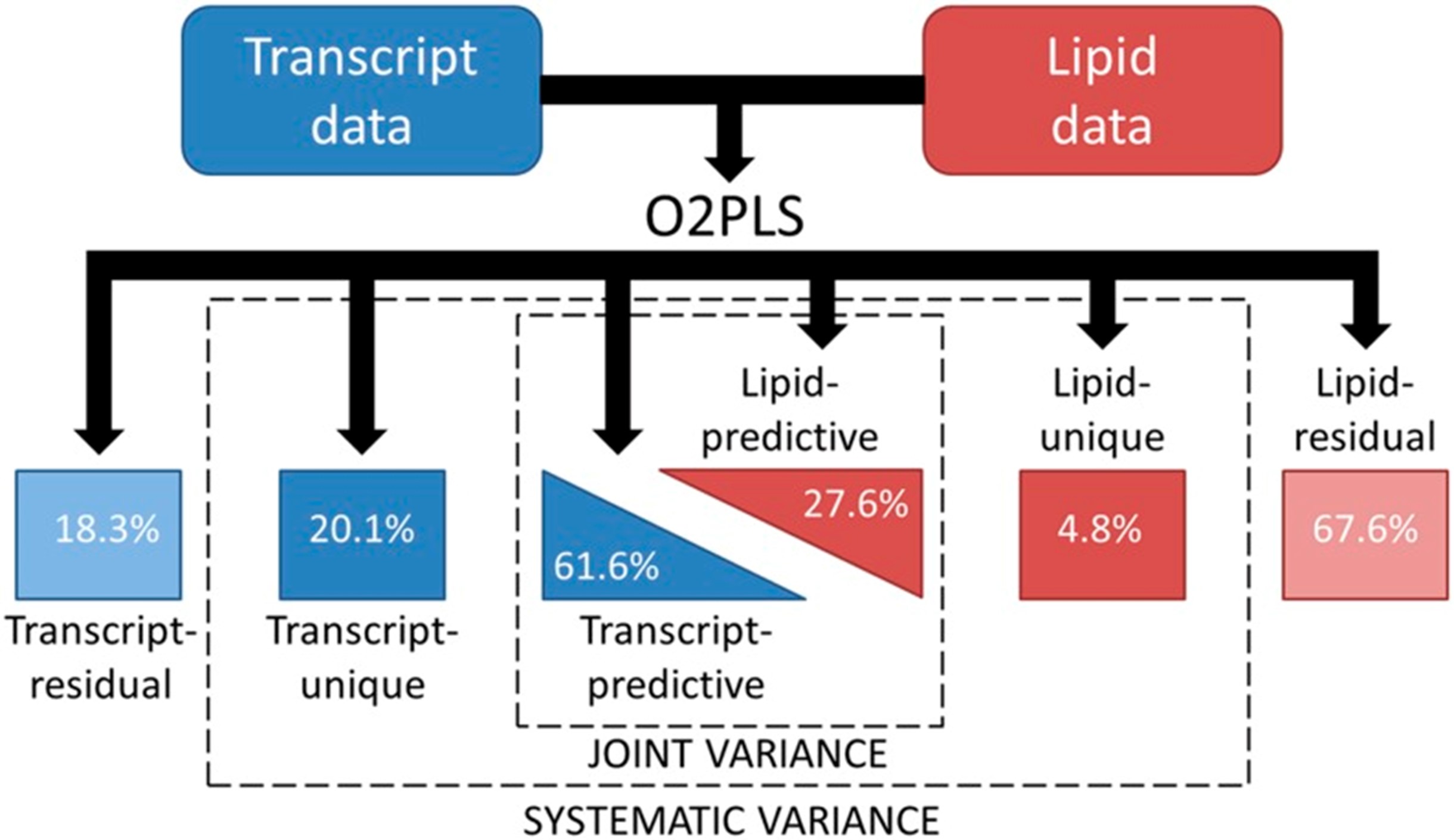
图3.7 O2PLS算法的示意图

（资料来源：Szymanski J., Brotman Y., et al. Linking Gene Expression and Membrane Lipid Composition of Arabidopsis. Plant Cell 26, 915–928 (2014).）

在O2PLS模型中，两个组学数据集\(\boldsymbol{X}\)（维度为 \(n \times p_1\)） 和\(\boldsymbol{Y}\)（维度为 \(n \times p_2\)）可以用以下隐变量分解的形式表示： $$\boldsymbol{X}=\boldsymbol{TW}^T+\boldsymbol{T}_{Y⊥}\boldsymbol{p}_{Y⊥}^T+\boldsymbol{E}_x\\\boldsymbol{Y}=\boldsymbol{UC}^T+\boldsymbol{U}_{X⊥} \boldsymbol{P}_{X⊥}^T+\boldsymbol{E}_y $$ 式中，组学数据集 \(\boldsymbol{X}\) 和\(\boldsymbol{Y}\)各自被分为三部分：1，两个组学相关的部分，其中，矩阵\(\boldsymbol{T}\)和\(\boldsymbol{U}\)为该部分的隐变量（成分）， 而\(\boldsymbol{W}\)和\(\boldsymbol{C}\)分别为\(\boldsymbol{T}\)和\(\boldsymbol{U}\)的载荷； 2，两个组学各自特有的部分，其中，隐变量\(\boldsymbol{T}_{Y⊥}\)和\(\boldsymbol{U}_{X⊥}\)分别代表\(\boldsymbol{X}\)，\(\boldsymbol{Y}\)特有的部分，与\(\boldsymbol{Y}\),\(\boldsymbol{X}\)线性无关； 3，残差项\(\boldsymbol{E}_X\)，\(\boldsymbol{E}_Y\)（图3.7）。

本项目结果图见结果文件 06_O2PLS分析/本部分包含以下结果：
├── 06_O2PLS分析
├── barplot.svg [依据载荷筛选出的重要基因和代谢物]
├── loading.svg [载荷图]
├── result.html [网页版O2PLS分析结果]
├── score.svg [隐变量得分图]
└── total.svg

图3.8 O2PLS分析

注：（a）依据载荷绝对值筛选出的重要的基因和代谢物图；（b）载荷图，代表载荷对不同主成分的贡献；（c）隐变量散点图，表示样本在PC1和PC2轴上隐变量的贡献度。

3.4.4 PLS-DA分析

上述三个模型均为无监督学习（Unsupervised Learning），无法将分组信息纳入到模型中。而PLS-DA模型^[20]属于监督学习（Supervised Learning）。监督学习的目标是获得一个包含特征的输入并返回对目标变量的预测^[21]。该模型可以同时整合转录组和代谢组（能整合多组不同类型的组学），分组信息也会被作为虚拟变量（Dummy Variable ，即哑变量）纳入模型中。此外，环境变量也可以纳入模型中（假定分组信息为包含分类变量n维向量；环境变量为包含连续型变量n维向量）。

本项目结果图见结果文件 07_PLS_DA分析/

本部分包含以下内容：
├── 07_PLS_DA分析
├── Comp.svg [载荷图]
├── Diablo.svg [两组学对应关系图]
├── auroc.svg [auc-roc曲线图]
├── biplot.svg [双序图]
├── loading.svg [载荷图]
└── plotVar.svg [相关性圈图]

图3.9 PLS-DA分析

注：（a）PLS-DA分析双序图，该图具有两套原点和单位向量方向相同的坐标系。图中散点代表隐变量而箭头代表载荷。散点表示样本在PC1和PC2轴上的隐变量的贡献度，对应Component坐标系（左下坐标轴）；从原点出发的箭头的端点表示载荷值，对应Eigenvector of Component坐标系（右上）。其生物学意义的解析见结题报告3.3.5 重要的图的解读；（b）隐变量散点图，其中Block1和Block2分别代表转录组和代谢组，散点表示样本在PC1和PC2轴上隐变量的贡献度；（c）依据载荷绝对值筛选出的重要的基因和代谢物图；（d）相关性圈图，代表载荷的分布情况。

3.4.5 重要的图的解读

本流程中涉及到的多元统计方法包括CCA, PLS, PLS-DA, O2PLS等。这些方法都将原始的数据分为隐变量（成分）及其所对应的载荷。双序图（biplot，有时也被译为双标图，图3.10（a））是一种集成图形，能同时展示隐变量和载荷的信息^[22]，注意在双序图中同时存在两套坐标系。在本流程结果的双序图中，用点表示样本，每个点在PC1和PC2轴上的投隐变量对隐变量的贡献度。从原点出发的箭头的端点表示载荷值。

这里重点介绍双序图的生物学意义。对于图中的任意两个样本点，从原点出发到样本点之间的夹角为锐角时，代表两个样本点所对应的样本具有相关基因表达谱（或代谢物丰度谱）。例如图A中SF268，SF295， SF539， SNB19， U251等在双序中相互接近，这些样本来源于同一个细胞系并具有相似的基因表达模式（图3.10（b））。夹角为钝角的具有相反的表达模式。若夹角接近直角，则表示这两个样本的表达谱不相关。两个箭头之间的夹角表示箭头所对应的基因（或代谢物）在不同样本的表达量的相关性。例如图中HEXB， WASL，GNS，PCBP4，DOCK7的夹角均为锐角，这些基因在不同样本呈现相似的表达量。在CNS和Melanoma两个细胞系的表达量高于Leikmeia。点和箭头之间的夹角代表表达量（或丰度）高低。角度越接近则该点所对应的样本中该基因（或代谢物）的表达量（或丰度）越高，例如样本SF268和基因PBCE1。反之，角度为钝角则意味着该点所对应的样本中该基因（或代谢物）的表达量（或丰度）较低，例如样本SF268和基因DPPA5^[5],[23]。

当仅需要展示载荷时，可使用相关性圈图（Correlation Circles Plot，图3.10（c））。在该图中，使用标准差对载荷进行缩放，从而使每个处理所有变量之和为1。图中展示了一个半径为1的单位圆，如果一个箭头的端点接近单位圆（半径接近1），则可认为该基因（或代谢物）能够很好的由隐变量1和2代表；反之，如果一个箭头的端点距离单位圆较远（半径小于1），则可能需要使用额外的隐变量展示该箭头所对应的基因或代谢物。有时也会用圆点来代替箭头表示载荷。

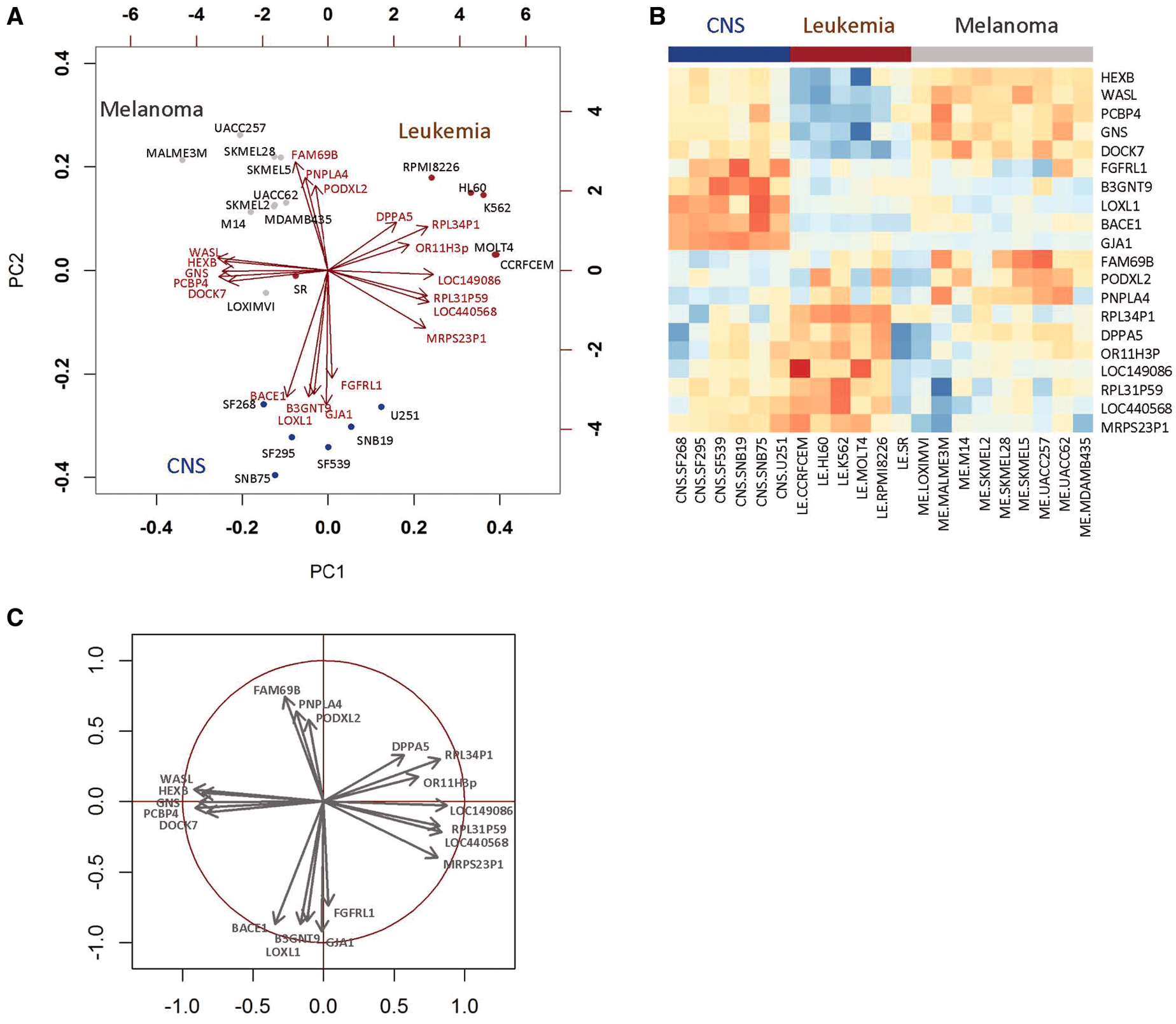
图3.10 统计模型部分的图示

注：a, 双序图；b, 相关性热图；c, 相关性圈图
（资料来源：Meng C., Zeleznik O., et al. Dimension Reduction Techniques for the Integrative Analysis of Multi-Omics Data. Brief. Bioinform. 17, 628–641 (2016).）

四 所用软件的版本

软件	版本
R	4.3.1
ggplot2	3.4.3
tidyr	1.3.0
dplyr	1.1.3
pheatmap	1.0.12
ggExtra	0.10.1
pathview	1.38.0
poolr	1.1.1
mixOmics	6.22.0
OmicsPLS	2.0.2
clusterProfiler	4.6.2
patchwork	1.1.3
R2HTML	2.3.3
Python	3.8.5
Pandas	1.1.2

表4.1 本流程使用软件的版本

五 参考文献

[1] Rohart F., Gautier B., et al. mixOmics: An R Package for Omics Feature Selection and Multiple Data Integration. PLOS Comput. Biol. 13, e1005752 (2017).

[2] Yan J., Risacher L., et al. Network Approaches to Systems Biology Analysis of Complex Disease: Integrative Methods for Multi-Omics Data. Brief. Bioinform. 19, 1370–1381 (2018).

[3] Kanehisa M., and Goto S. KEGG: Kyoto Encyclopedia of Genes and Genomes. Nucleic Acids Res. 28, 27–30 (2000).

[4] Butte J., Tamayo, et al. Discovering Functional Relationships Between RNA Expression and Chemotherapeutic Susceptibility using Relevance Networks. Proc. Natl. Acad. Sci. U. S. A. 97, 12182–12186 (2000).

[5] González I., Cao, et al. Visualising Associations between Paired ‘Omics’ Data Sets. BioData Min. 5, 19 (2012).

[6] Luo W., and Brouwer C. Pathview: An R/Bioconductor Package for Pathway-Based Data Integration and Visualization. Bioinformatics 29, 1830–1831 (2013).

[7] Kanehisa M., Furumichi M., et al. KEGG: New Perspectives on Genomes, Pathways, Diseases and Drugs. Nucleic Acids Res. 45, D353–D361 (2017).

[8] Koonin V. Orthologs, Paralogs, and Evolutionary Genomics. Annu. Rev. Genet. 39, 309–338 (2005).

[9] Khatri P., Sirota M. and Butte A. J. Ten Years of Pathway Analysis: Current Approaches and Outstanding Challenges. PLoS Comput. Biol. 8, e1002375 (2012).

[10] Goeman J., and Bühlmann P. Analyzing Gene Expression Data in Terms of Gene Sets: Methodological Issues. Bioinforma. Oxf. Engl. 23, 980–987 (2007).

[11] Subramanian A., Tamayo P., et al. Gene Set Enrichment Analysis: A knowledge-Based Approach For Interpreting Genome-Wide Expression Profiles. Proc. Natl. Acad. Sci. 102, 15545–15550 (2005).

[12] Wu T., Hu E., et al. ClusterProfiler 4.0: A Universal Enrichment Tool for Interpreting Omics Data. The Innovation 2, 100141 (2021).

[13] Canzler S., and Hackermüller J. multiGSEA: a GSEA-Based Pathway Enrichment Analysis for Multi-Omics Data. BMC Bioinformatics 21, 561 (2020).

[14] Cinar O., and Viechtbauer W. The poolr Package for Combining Independent and Dependent p Values. J. Stat. Softw. 101, (2022).

[15] Meng C., Zeleznik O., et al. Dimension Reduction Techniques for the Integrative Analysis of Multi-Omics Data. Brief. Bioinform. 17, 628–641 (2016).

[16] Hong S., Chen X., et al. Canonical Correlation Analysis for RNA-seq Co-Expression Networks. Nucleic Acids Res. 41, e95 (2013).

[17] Witten M., and Tibshirani J. Extensions of Sparse Canonical Correlation Analysis with Applications to Genomic Data. Stat. Appl. Genet. Mol. Biol. 8, 28 (2009).

[18] Krishnan A., William J., et al. H. Partial Least Squares (PLS) Methods for Neuroimaging: A Tutorial and Review. NeuroImage 56, 455–475 (2011).

[19] Szymanski J., Brotman Y., et al. Linking Gene Expression and Membrane Lipid Composition of Arabidopsis. Plant Cell 26, 915–928 (2014).

[20] Singh A., Shannon C., et al. DIABLO: An Integrative Approach for Identifying Key Molecular Drivers from Multi-Omics Assays. Bioinformatics 35, 3055–3062 (2019).

[21] Eraslan G., Avse Ž., et al. Deep Learning: New Computational Modelling Techniques for Genomics. Nat. Rev. Genet. 20, 389–403 (2019).

[22] Gabriel R. The Biplot Graphic Display of Matrices with Application to Principal Component Analysis. Biometrika 58, 453–467 (1971).

[23] Oyedele F., and Lubbe S. The Construction of a Partial Least-Squares Biplot. J. Appl. Stat. 42, 2449–2460 (2015).